実務でのChatGPT（統計 有意差検定＋箱ひげ図：Data Analyst）

「成形工程改善したんだって？」

「そう、周囲の温度の影響を受けているから、センサーを付けて制御したの」

「で、結果は？」-> このような時は、有意性を知りたいですよね。

次のデータ；成形工程の何らかのアウトプットを以下として、解析を進めます。
＊データは、csvファイルをアップしました。　

ここでは、最終的に平均値は有意性を有するか否かを検定することが目的です。この際、検定の流れは以下のようになります。

1. データが正規分布に従うか？
2. ばらつきに有意差があるか？
3. 平均値に有意差があるか？

この手順の理由は、データに正規性があるかどうかで、ばらつきの有意性を確認する検定の種類がかわり、またまた、ばらつきに有意性があるかどうかで、平均値の検定の種類も変わるからです。

GPTsでData Analyst というのがあり、データ分析、統計、プログラミングに関連する質問やタスクに対応しています。このようなややこしいのは、そういう事情をプロンプトで表現します。

ファイルの「改善前」「改善後」のデータで、データが正規分布に従うか検定後、その結果に応じて、ばらつきに有意差があるか検定してください。次にばらつきの検定の結果に応じて、平均値に有意差があるか検定してください。また、p値も教えてください。それぞれ有意水準は5%とします。

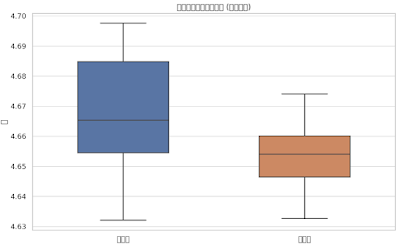
実際にばらつきは小さくなっており、p値からが有意であることが伺えます。平均値は5%有意水準では有意ではありませんが、実験レベルのデータならば考慮すべきp値です。
＊回答でのそれぞれの検定の区切りでは、pythonのcodeが示されています。

結局のことろ、ばらつきが小さくなっており、製造系では望ましい結果でしょう。

・・・会話で検定ができてしまうんですね。

[追記]
＊ファイルをアップした最初のプロンプトで「このファイルを分析してください」と入力すると、「改善前」「改善後」それぞれの統計量が回答されます。

ここで、ヒストグラム、箱ひげ図による視覚化の提案があるので、箱ひげ図を選択すると―

＜過去の統計解析に関する投稿＞

• 有意性の判定―p-値（よくある2つの疑問）
• 変更点が原因であると推定するのは新入社員の仕事です。
• スペックの落とし穴。
• 相関関係と因果関係